Logistic Regression: Diagnostics

Logistic Regression: Diagnostics

One assumption of logistic regression is that the random component of the model is binomial. All subjects with the same set of X values share the same probabilities of having each of the two possible outcomes. So the dependent variable Y=1,0.

Expected value of Y known as predicted mean value  is

Variance of Y known as model-specified variance  is:

In ordinary least squares regression, we can have outliers on X or Y variables. But we can only consider extreme values on X with logistic regression because Y could be 1 or 0 only.

1. Pearson residuals

As random variable Y, there is Pearson Residuals(Res) or standardized residuals.

R code:

> #residuals

> data1<-data1[order(data1[,'lastage']),]

> lr<-glm(mscd~eversmk+ns(lastage,3), data=data1, family=binomial(link='logit'))

> #expected value of Y

> mean_Y<-predict(lr, type='response')

> #standard error of Y

> se_Y<-sqrt(mean_Y*(1-mean_Y))

> #pearson residuals

> res<-(data1$mscd-mean_Y)/se_Y

> par(mfrow=c(1,2))

> #Y~X

> plot(x=data1$lastage, y=data1$mscd, pch=20)

> points(x=data1$lastage, y=mean_Y,  col='red',pch=20 )

> #pearson residuals

> plot(x=mean_Y, y=res, pch=20, xlab='Expected value of Y',        ylab='Pearson residuals')

> abline(h=0)

2. Deviance residuals

The below equation is the deviance statistics. In particular, if , the deviance is minimized to 0.

Regarding the maximum likelihood estimation, The function 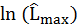should be close to 0 denoted as .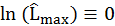

Deviance residuals:

R code:

> #deviance statisticcs determined by formula

> (-2*sum((mean_Y*log(mean_Y/(1-mean_Y))+log(1-mean_Y))))

[1] 7339.494

> #deviance residuals given by glm()

> summary(lr)$deviance

[1] 7339.494

> #deviance residuals

> dev_vector=-2*(data1$mscd*log(mean_Y)+(1-data1$mscd)*log(1-mean_Y))

> dev=ifelse(data1$mscd==1, sqrt(dev_vector), -sqrt(dev_vector))

> #plot

> par(mfrow=c(1,1))

> plot(x=mean_Y, y=dev, pch=20, xlab='Expected value of Y',

+      ylab='Deviance residuals')

> abline(h=0)

3. Leverage points

A common diagnostic index for extreme X values is leverage (diagonal of hat matrix) denoted as hij.