Logistic regression: Maximum Likelihood Estimation of coefficients

Logistic regression: Maximum Likelihood Estimation

1. Maximum likelihood estimation

In Logistic regression model, the response variable yi (y=1,0) is independent variable and follows
 Bernoulli distribution: yi ~ B(p, p(1-p)). And logit function of logistic regression model:

So

The derivatives:

The likelihood function of β given yi (i=1,2,…n) is

Set the above equation to equal in order to maximize likelihood.

Here, is variance-covariance matrix set as V.

Consider Newton-Raphson method given a function f(x):

In terms of the maximum likelihood function

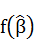
The equations of likelihood estimation:

Iteratively Re-weighted Lease Squares (IRLS)

Calculate coefficients values of when k=0.

Calculate V()