Mathematics: Geometric Series

Mathematics: Geometric Series

1. Definition of Geometric Series

Geometric Series is

Proof :

if |x|<1 and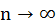

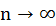
Consider the two functions below, and therefore there is Y>0 if 0<p<1. but log(Y) is 0~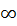 
if log(1/(1-p)), and - if log(p/(1-p))

R code

p<-seq(0,1, 0.001)

#

plot(x=p, y=1/(1-p), ylim=c(0,100), type='l', lwd=5,col='blue')

points(x=p, y=p/(1-p), type='l', lwd=2,col='red')

abline(v=1)

text(.2,80, 'blue:f(p)=1/(1-p), 0<p<1')

text(.2,60, 'red:f(p)=p/(1-p), 0<p<1')

#log function

plot(x=p, y=log(1/(1-p)), ylim=c(-8,8), type='l', lwd=5,col='blue')

points(x=p, y=log(p/(1-p)), type='l', lwd=2,col='red')

2. Variants of geometric series

Proof

So

if |x|<1 and , So