Tiezheng Yuan Ph.D.: Matrix operations

Matrix operations

matrix transpose

Product matrix and matrix transpose, X'pxnXnxp=Zpxp.

X' is matrix X transpose. Z is symmetrical matrix

> t(X)%*%X

[,1] [,2]

[1,] 10 2

[2,] 2 8

> X%*%t(X)

[,1] [,2] [,3]

[1,] 5 3 4

[2,] 3 9 0

[3,] 4 0 4

There are some rules.

(X')'=X

(X+Y)'=X'+Y' equally (X'+Y)=X+Y'

(XY)'=Y'X' equally (X'Y)'=Y'X

(ABC)'=C'B'A'

Product of vector matrix transpose (is a vector) and vector matrix is sum square

Product of vector matrix and vector matrix transpose is a symmetric matrix

Symmetric matrix of invert

set

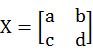, so invert matrix

R code

> (X<-matrix(c(1,3,7,2), ncol=2))

[,1] [,2]

[1,] 1 7

[2,] 3 2

> solve(X)#the function solve() invert matrix X

[,1] [,2]

[1,] -0.1052632 0.36842105

[2,] 0.1578947 -0.05263158

Matrix invert make sense one if the matrix is a diagonal matrix. So X'X could be diagonal matrix
if X is not a diagonal matrix. There are some rules.

XX-1=X-1X=I

(A-1)-1=A

(A')-1=(A-1)'

(XY)-1=Y-1X-1

(ABC)-1=C-1B-1 A-1

Linear algebra of AY=C

Hat matrix: H=X(X'X)-1X'

> X

[,1] [,2]

[1,] 1 2

[2,] 3 0

[3,] 0 2

> (H=X%*%solve(t(X)%*%X)%*%t(X))

[,1] [,2] [,3]

[1,] 0.5263158 0.1578947 0.4736842

[2,] 0.1578947 0.9473684 -0.1578947

[3,] 0.4736842 -0.1578947 0.5263158

With H=X(X'X)-1X, hat matrix is n x n matrix. The diagonal vector is known as leverage scores vector.
There is

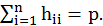n is number of observations, and here n=3. p is the number of
coefficients. Due to

, hii express how much observations yi has impact on expected
value of yi. A large hii indicates that the i th case is distant from the average X values and more
leverage. In this example, the highest leverage score is 0.9473684. The theoretical ideal result for
H matrix would all elements are the same, of which hii =p/n. If an element in the hat matrix diagonal
is twice as great as the average value p/n, the observations should be considered a leverage point
and one ought to be cautious about it.

There are some features of hat matrix.