Linear Regression: Residuals

Linear Regression:  Residuals

Call:

lm(formula = wt ~ age, data = d)

Residuals:

   Min     1Q Median      3Q Max

-3.7237 -0.8276  0.1854 0.9183 4.5043

Coefficients:

           Estimate Std. Error t value Pr(>|t|)    

(Intercept) 5.444528   0.204316 26.65 <2e-16 ***

age         0.157003 0.005845   26.86 <2e-16 ***

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.401 on 183 degrees of freedom

Multiple R-squared:  0.7977,    Adjusted R-squared:  0.7966

F-statistic: 721.4 on 1 and 183 DF,  p-value: < 2.2e-16

Here is a linear regression model with weight denoted as Y (dependent variable), and age denoted as X (independent variable):

Y=β0+β2X+ε

Here, residuals are denoted by ε, and ε ~ N(0, σ2). So

E(ε)=0 and Var(ε)=σ2                       (1)

But ε is unobserved. So there is OLS residuals 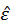as showed by the summary of lm() in the inception. 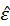is difference between yi and

Proof E()=0             (2)

Because

So E()=0

Proof Var()= σ2             (3)

So

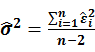Proof if set              (4)

The below is the R code for showing features of OLS residuals :

> residuals<-d$wt-predict(lm1)

> quantile(residuals)

       0%  25% 50%        75% 100%

-3.7236731 -0.8275872  0.1854405 0.9183452 4.5043396

The next calculate variance of OLS , but σ2 is unknown. So calculate 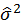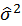based on proof (4).

> (sqrt(sum((residuals)^2)/183))

[1] 1.400649