Tiezheng Yuan Ph.D.: Linear Regression: Estimate coefficients in simple linear regression

Linear Regression: Estimate coefficients in simple linear regression

Call:

lm(formula = wt ~ age, data = d)

Residuals:

Min 1Q Median 3Q Max

-3.7237 -0.8276 0.1854 0.9183 4.5043

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 5.444528 0.204316 26.65 <2e-16 ***

age 0.157003 0.005845 26.86 <2e-16 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.401 on 183 degrees of freedom

Multiple R-squared: 0.7977, Adjusted R-squared: 0.7966

F-statistic: 721.4 on 1 and 183 DF, p-value: < 2.2e-16

Here is a linear regression model with weight denoted as Y (dependent variable), and age denoted as X (independent variable):

Y=β0+β1X+ε

The most commonly used for estimating the unknown parameters β0 and β1 is ordinary least square (OLS) which minimize the Residuals Sum of Squares (RSS). As showed by the above, β0 denoted as intercept and β1denoted as slope are 5.444528 and 0.157003. The best-fit value of the slope means that age increase by 1.0 unit, the average weight is expected increased by 5.44 grams.

Proof OLS

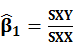and

So,

, and

let the formula above equal to 0 in order to minimize RSS:

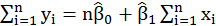
Solve the equation systems with two unknown parameters using linear algebra matrix.

So,

Set

So,

Here are the R code the calculate β0 and β1, which are equal to the estimations by function lm().

> x.mean=mean(d$age)

> y.mean=mean(d$wt)

> SXX=sum((d$age-x.mean)^2)

> SYY=sum((d$wt-y.mean)^2)

> SXY=sum((d$age-x.mean)*(d$wt-y.mean))

> (beta1=SXY/SXX) # β1

[1] 0.1570031

> (beta0=y.mean-beta1*x.mean) #β0

[1] 5.444528

The next, we consider expected value and variance of β1 andβ0.

First set

Then

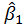and

are unbiased estimator of β0 and β1

Proof

Proof

Proof variance

Proof variance

Because is σ2 unknown, there is therefore standard error of

and

Here are the R codes for calculating standard error of coefficients. The code gave the identical coefficients showed by summary of linear regression models.

> (SXX<-sum((d$age-mean(d$age))^2))

[1] 57416.38

> (delta2<-sum(residuals^2)/183)#OLS RSS

[1] 1.961817

> (sqrt(delta2/SXX))#standard error of beta1

[1] 0.005845362

> (x.mean=mean(d$age))

[1] 30.18919

> (n<-nrow(d))

[1] 185

#standard error of beta0

> (sqrt(delta2*((1/n)+(x.mean)^2/SXX)))

[1] 0.2043157

The next, we deduct confidence interval at level α. The degree of freedom is 183.

We suppose

and

denoted as Gaussian distribution. So

The population σ2 is unknown. We could estimate OLS σ2 (). Use the standard error of

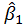and

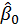instead of standard deviation of β1 andβ0.

So (1-α)% confidence interval of

and

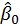H0:

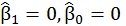implies that no linear relationship exists between X and Y.

H1:

Under H0:

So t statistics:

Here are the R code

> (beta1=SXY/SXX)

[1] 0.1570031

> (se_beta1<-sqrt(delta2/SXX))#se of beta1

[1] 0.005845362

#t statistics of beta1

> (t_beta1<-beta1/se_beta1)

[1] 26.85943

> #p value

> (pt(t_beta1, 183, lower.tail=F))

[1] 1.05584e-65

> (se_beta0<-sqrt(delta2*((1/n)+(x.mean)^2/SXX)))#se of beta0

[1] 0.2043157

> (beta0=y.mean-beta1*x.mean)

[1] 5.444528

> #t statistics of beta0

> (t_beta0<-beta0/se_beta0)

[1] 26.64762

> #p value

> (pt(t_beta0, 183, lower.tail=F))

[1] 3.352655e-65

Finally, the analysis of variance (ANOVA) is another method to test for the significance of regression. Test statistic for the F-test on the regression model. F-statistics tests for a significant linear regression relationship between the response variable and the predictor variables.

H0: