Multiple Linear regression:
Coefficient estimation of MLR
Coefficient estimation of MLR
Suppose that there is linear relationship between variables X and Y. So consider a multiple variate
linear regression model (MvLR)
linear regression model (MvLR)
Remember the below formula
E(Y|X)=βX
Var(Y|X)= σ2I
- Maximum likelihood function and Least square
Under Gaussian multiple density distribution, εi is random independent variables. We have a Gaussian
distribution
 . So
. So
distribution
Minimize the sum of squared residuals (RSS) using Ordinary Least Square method (OLS), and
estimate unknown or observed parameters β and ε, which was denoted as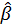
 and
and 
 .
.
estimate unknown or observed parameters β and ε, which was denoted as
Due to 
 ,
,
So

So
So, 

Due to matrix calculus theorem, and X'X is symmetric matrix, so X'X=(X'X)'=XX', and (X'X)-1X'X=I.
The derivatives
set 
 . So
. So 

Here is a case study of multiple variables linear regression
> lm2<-lm(wt~age+ht, data=d)
> summary(lm2)
Call:
lm(formula = wt ~ age + ht, data = d)
Residuals:
Min 1Q Median 3Q Max
-2.48498 -0.53548 0.01508 0.51986 2.77917
Coefficients:
Estimate Std. Error t value Pr(>|t|) 
(Intercept) -8.297442 0.865929 -9.582 <2e-16 ***
age 0.005368 0.010169 0.528 0.598
ht 0.228086 0.014205 16.057 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9035 on 182 degrees of freedom
Multiple R-squared: 0.9163, Adjusted R-squared: 0.9154
F-statistic: 995.8 on 2 and 182 DF, p-value: < 2.2e-16
> coef(lm2)
(Intercept) age ht
-8.297442239 0.005368228 0.228085501
So the coefficients of 

Calculate 
 Based on the formula
Based on the formula

Here are the R code for calculating 

> X<-cbind(rep(1, nrow(d)), as.matrix(d[,c('age','ht')]))
> Y<-as.matrix(d$wt)
> library(MASS)
> ginv(t(X)%*%X)%*%t(X)%*%Y
[,1]
[1,] -8.297442239
[2,] 0.005368228
[3,] 0.228085501
- Gauss-Markov Theorem.
Here, we am going to discuss the expected value, variance and variance-covariance of coefficients.
Gauss-Markov Theorem: OLS estimator is the Best Linear, Unbiased, and efficient Estimator (BLUE).
There are three main proofs regarding the statements.
Gauss-Markov Theorem: OLS estimator is the Best Linear, Unbiased, and efficient Estimator (BLUE).
There are three main proofs regarding the statements.
is unbiased estimator of β:
proof 
 .
.
Assumption: Y=Xβ+ε, E(ε|X)=0, and X has rank k (no perfect collinearity).
Because (X'X)-1X'X=I and E(ε)=0, and Iβ=βI=β
proof variance of 
 .
. 


has linear relationship with β
Proof
has minimal variance among all linear and unbiased estimators.
Proof variance-covariance matrix of the OLS estimates:


With linear algebra theorem COV(X)=E[(X-E(X))(X-E(X))'], and 
 . So
. So
Because 
 and Y=Xβ+ε. So
and Y=Xβ+ε. So
So 

Because 
 , So
, So
Because σ2 is unknown, replace σ2 with 
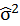 when n is huge. So
when n is huge. So
> #standard error of OLS_beta
> OLS_residuals<-Y-X%*%OLS_beta
> (OLS_var<-as.numeric(t(OLS_residuals)%*%OLS_residuals/182))
[1] 0.8162765
> OLS_var*diag(1, 3)
[,1] [,2] [,3]
[1,] 0.8162765 0.0000000 0.0000000
[2,] 0.0000000 0.8162765 0.0000000
[3,] 0.0000000 0.0000000 0.8162765
> #variance-covariance matrix
> (var_cov<-OLS_var*diag(1, 3)%*%ginv(t(X)%*%X))
[,1] [,2] [,3]
[1,] 0.749832532 0.0076531233 -0.0121572259
[2,] 0.007653123 0.0001034006 -0.0001341481
[3,] -0.012157226 -0.0001341481 0.0002017823
> #standard error of OLS beta
> (se_beta<-sqrt(diag(var_cov)))
[1] 0.86592871 0.01016861 0.01420501
Here are the 95% confidence intervals of
| |
> (t95<-qt(0.975, df=182, lower.tail=F))
[1] 1.973084
> data.frame('beta'=OLS_beta, 'lower_bound'=OLS_beta-t95*se_beta,
+ 'upper_bound'=OLS_beta+t95*se_beta)
beta lower_bound upper_bound
1 -8.297442239 -10.00599239 -6.58889209
2 0.005368228 -0.01469529 0.02543175
3 0.228085501 0.20005782 0.25611318
| |
|
- Normality and Significance test of coefficients
The test is used to check the significance of individual regression coefficients in the multiple linear
regression model. Adding a significant variable to a regression model makes the model more
effective, while adding an unimportant variable may make the model worse. The hypothesis
statements to test the significance of a particular regression coefficient.
regression model. Adding a significant variable to a regression model makes the model more
effective, while adding an unimportant variable may make the model worse. The hypothesis
statements to test the significance of a particular regression coefficient.
Under the CLM assumptions, we suppose 
 denoted as Multivariate Gaussian distribution (MVG)
denoted as Multivariate Gaussian distribution (MVG)
with mean β and variance-covariance matrix σ2(X'X)-1. So
with mean β and variance-covariance matrix σ2(X'X)-1. So
We could obtain a standard normal distribution of an OLS estimator given k th coefficient:
The population σ2 is unknown. We could estimate OLS σ2 (). Use the standard error of 
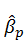
instead of standard deviation of β1 andβ0.
instead of standard deviation of β1 andβ0.
So (1-α)% confidence interval of 
 and
and 
 .
.
H0: 
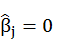 implies that no linear relationship exists between X and Y.
implies that no linear relationship exists between X and Y.
H1: 

Under H0:
So t statistics:
Here are the R code
#t-statistics
> (t_stat<-(OLS_beta-0)/se_beta)
[,1]
[1,] -9.5821309
[2,] 0.5279217
[3,] 16.0566930
#p values
> pt(t_stat, df=182, lower.tail=T)
[,1]
[1,] 3.635395e-18
[2,] 7.009016e-01
[3,] 1.000000e+00
Then we could expand the method. Suppose

And 
 is denoted as Gaussian distribution. So
is denoted as Gaussian distribution. So
There is variance-covariance matrix 

Regarding 
 , there are variance
, there are variance 
 , and
, and
covariance
 . So
. So
covariance
So 95% CI of 

So 

No comments:
Post a Comment