Multiple Linear regression: Predicted Values
> lm2<-lm(wt~age+ht, data=d)
> summary(lm2)
Call:
lm(formula = wt ~ age + ht, data = d)
Residuals:
Min 1Q Median 3Q Max
-2.48498 -0.53548 0.01508 0.51986 2.77917
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -8.297442 0.865929 -9.582 <2e-16 ***
age 0.005368 0.010169 0.528 0.598
ht 0.228086 0.014205 16.057 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9035 on 182 degrees of freedom
Multiple R-squared: 0.9163, Adjusted R-squared: 0.9154
F-statistic: 995.8 on 2 and 182 DF, p-value: < 2.2e-16
The estimated coefficient 
 using OLS
using OLS
R code:
#matrix of independent variables
> X<-cbind(rep(1, nrow(d)), as.matrix(d[,c('age','ht')]))
> head(X)
age ht
446 1 1 52.4
671 1 1 53.6
241 1 2 56.2
261 1 2 54.7
301 1 2 54.1
196 1 3 57.0
> dim(X)
[1] 185 3
#matrix of depencent variable:
> Y<-as.matrix(d$wt)
> dim(Y)
[1] 185 1
#degree of freedom
> (df=nrow(X)-length(coef(lm2)))
[1] 182
#OLS_beta: beta0, beta1, beta2
> (OLS_beta<-ginv(t(X)%*%X)%*%t(X)%*%Y)
[,1]
[1,] -8.297442239
[2,] 0.005368228
[3,] 0.228085501
#hat matrix
> H<-X%*%ginv(t(X)%*%X)%*%t(X)
> dim(H)
[1] 185 185
- Response variable
Consider a multiple variate linear regression model (MvLR)
Here, εi ~ N(0, σ2), or ε ~ MVG (0, σ2I). So E(ε)=0, Var(ε)= σ2I. Now consider the values of response variable yi or Yn×1.
Here, Xβ is fitted value and random variable ε is supposed to follow normal distribution. Therefore the values of the function Xβ+ε should follow normal distribution:
- Predicted values of dependent variable
So expected value of Y is
set hat matrix 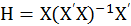
 So
So 
 .
.
H is symmetric (There is linear algebra theorem: 
 ):
):
H is independent:
R code:
> OLS_Y=H%*%Y
> head(OLS_Y)
[,1]
446 3.659607
671 3.933308
241 4.531700
261 4.189571
301 4.052719
196 4.719536
The n x n matrix H is known as the hat matrix simply because it maps y into 
 , and H is only determined by X regardless of Y. The element hij of H has a direct interpretation as the amount of influence on
, and H is only determined by X regardless of Y. The element hij of H has a direct interpretation as the amount of influence on 
 by y. hij points out which the value of y has a large impact on the fit.
by y. hij points out which the value of y has a large impact on the fit.
The diagonal elements of H hii, are called leverages and satisfy
where p is the number of coefficients, and n is the number of observations (rows of X) in the regression model. HatMatrix is an n-by-n matrix in the Diagnostics table.
- Confidence Interval of predicted value
There is OLS 
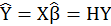 where linear relationship between predicted value and coefficient is
where linear relationship between predicted value and coefficient is 
 . Because
. Because 


 . So
. So
Implement delta method, so
If 
 is unknown, estimate
is unknown, estimate 
 with
with
 . p is the number of coefficients, and n is the number of observations.
. p is the number of coefficients, and n is the number of observations.
95% of 
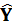
> #residuals sum of squares
> (RSS<-t(Y)%*%(diag(1,nrow(H))-H)%*%Y)
[,1]
[1,] 148.5623
> vcov_Y<-as.numeric(RSS/(nrow(H)-2-1))*H
> #variance-covariance matrix of OLS-Y
> dim(vcov_Y)
[1] 185 185
> #standard error of OLS-Y
> se_Y<-sqrt(diag(vcov_Y))
> #95%CI
> (t95<-qt(0.975, df=182, lower.tail=F))
[1] 1.973084
>CI=data.frame('exp_Y'=exp_Y,'lower_bound'=exp_Y-t95*se_Y, 'upper_bound'=exp_Y+t95*se_Y)
> head(CI)
exp_Y lower_bound upper_bound
446 3.659607 3.311358 4.007855
671 3.933308 3.607185 4.259432
241 4.531700 4.242070 4.821329
261 4.189571 3.875997 4.503145
301 4.052719 3.728534 4.376904
196 4.719536 4.437238 5.001834
> CI<-CI[order(CI$exp_Y),]
> plot(x=1:nrow(CI), y=CI$exp_Y, type='l', ylab='Expected value of OLS-Y',
+ main='95% CI of OLS-Y')
> points(x=1:nrow(CI), y=CI$lower_bound, type='l', col='blue' )
> points(x=1:nrow(CI), y=CI$upper_bound, type='l', col='red' )
Based on linear combination, let say H matrix is i*j (i=j), whose variance and covariance of any cells could be hij. The formula above given dependent variables Y, the expected value of yi could be written as
Here is a plot of residuals (
#plot of expected value of Y~ OLS-residuals
plot(x=H%*%Y, y=(diag(1,nrow(H))-H)%*%Y,
xlab='Predicted value (OLS_Y)', ylab='Residuals(OLS_e)')
abline(h=0)
|
The next
No comments:
Post a Comment